SOCIAL ENTROPY: A
PARADIGMATIC APPROACH
OF THE SECOND LAW OF
THERMODYNAMICS
TO AN UNUSUAL
DOMAIN
Alfredo Palomino
Infante
Prof. Facultad de
Química e Ingeniería Química, UNMSM
James H.L.Lawler
Honorary Professor of San Marcos University,
Lima Perú
President of Nexial Institute, Dallas, USA
jhlawr@wmconect.com
SUMMARY
A pseudo state function, the “Social
Entropy” (SE) is defined in order to show the application of the
second law of thermodynamics to the human social behavior. This is achieved
under the assumption that such property (SE) is equivalent to the degree
of social dissatisfaction (SD), of certain social,
economic, or political system. Hence, a Boltzmann type equation is used
after simplifying it with Stirling formula , to obtain a rough estimative of
the amount of the relative SE in a determined place and
moment of history .
A case study related to the
Peruvian society has been used here to demonstrate our hypothesis that the
social entropy tends to increase with time. Similarly the degree
of disorder of a thermodynamic system increases with time. Generally
speaking we observe so far that the degree of disorder is a manifestation of
the social dissatisfaction within the limits of the system.
CONTENTS
1
Introduction
2
Classical Thermodynamics
3
Un Unsuspected Visitor
4
Social Entropy as Pseudo
State Function
5
Formulating the
Relationship to Calculte Social Entropy
6
A Case Study to Calculate
Social Entropy
7
Discussion and Analysis
8
Concluding Remarks
9
References
1.
Introduction
We present a rather unusual
application of the Second Law of Thermodynamics, in order to help us to
understand the increase of entropy in a human society. To do this a Boltzman
type equation is used after simplifying it using the Stirling formula. Here,
the state of a human society as a system is described by the degree of
dissatisfaction or satisfaction with the social, political and economic rules
of a country. The human social behavior may be measured and expressed
quantitatively by using a reliable poll. The results obtained with such
relationship shows that the Second Law of Thermodynamics may be successfully
applied to understand the human social behavior.
2.
Classical Thermodynamics
Let us recall some definitions of classical
thermodynamics:
“The mathematical treatment
of the relation of the heat to mechanical and other forms of energy. Its chief
applications are to heat engines and chemical reactions”.(1)
“...a physical discipline
examining inter - conversions between different kinds of energy and the
exchange of energy between systems, specially in the form of heat”.(2)
2.1
Some Fundamental Concepts of Classical Thermodynamics
Closed System:
In classical thermodynamics, a closed system is chosen and must clearly be
defined for the purpose of the study to establish the boundary within the
larger universe.
Energy, E:
Energy is defined as the capacity of a body for doing work.
Heat, Q:
Heat is that form of energy that flows when a hot system is put in thermal
contact with a cold system. This type of energy flow is sustained by the
difference of temperature between the two systems as a driving force.
Work,
W :
Work is any mechanical interaction between the
system and its surroundings. This has (or could have) as an equivalent
effect of the raising of a weight (force times distance moved) or more
commonly this may be expressed as pressure times a change in volume PV
in the system interacting with its surroundings. Heat energy and work energy
are forms of energy that matter does not intrinsically possess, but they
are forms of energy that flow between a system and its surroundings.
Internal energy, U:
is the amount of energy which is stored in a body and accounts for the
movements of atoms which constitutes the matter, it is a state function of the
system and its value depends upon the chosen standard state. It is essentially
the same as E for a closed system.
Enthalpy, H:
Enthalpy is the sum of all energy types and is usually defined as total of
internal energy and work by the following relationship: H=U+PV, where, H is
enthalpy, P is the pressure and V is volume of the system. H is a
state function.
Entropy, S:
It is defined for thermal reversible processes by the equation
DS=DQ/T
. Statistically Boltzman as will be shown later also defines entropy in terms
of disorder. Entropy is a state function.
Gibbs Free Energy, G:
It is defined as
G=H-TS. where T is the temperature of the system, and G is the total energy
less that energy (TS) which is unavailable. The difference is the energy that
is available and also represents a state of the system.
Chemical Potential,
m:
Lets write the following relationship
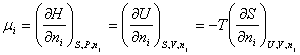
Through this definition it was
possible to open new applications of the second law of thermodynamics to
chemistry , chemical engineering, biology and other fields. It let us
characterize the state of a reacting as well as phase changing systems among
others.
2.2
First Law of Thermodynamics
This law establishes that the
energy in the universe remains constant. Thus energy only transformed from one
type into another. If we restrict it to a closed system we may write:
dU = DQ + DW
(1)
“D “:stands for differential of
functions that are not state variables, and “d” for differential of state
variable. This law is a postulated and doesn’t need any further demonstration.
2.3
Second Law of Thermodynamics
The entropy production
represents the existence of irreversibility. The second law may be stated in
several equivalent ways, such as that the entropy tends to increase with time
in any naturally occurring process. Thus, entropy is necessarily positive or
zero
For any process it is possible
to write:
dS
³ DQ/T
(2)
“=” stands for a reversible
process and “
>” for irreversible
process.
ã
Alfredo Palomino Infante/Prof. UNMSM
Boltzman gives statistical interpretation of the Second Law of Thermodynamics.
He
established that the entropy (S)
of a system may be used to characterize the thermodynamic probability (W)
of the state of such system. The relationship between these variables is
expressed by the following equation.
S= R ln
W = kNo ln
W
(3)
Fig. 1 Distribución aleatoria de
partículas según modelo de Boltzmann

Where k is the Boltzmann
constant, k=R/No, No being the Avogadro number.
2.4
Third Law of Thermodynamics
 Planck
(1900) stated that every system whose temperature approaches zero (T
+0) has zero entropy (S=0). This means that at such low temperature movement
ceases and full order is achieved in a system. Eq. (4) is a mathematical way
of expressing this statement. This law is also a postulate, just
exactly as the first and second laws are.
Planck
(1900) stated that every system whose temperature approaches zero (T
+0) has zero entropy (S=0). This means that at such low temperature movement
ceases and full order is achieved in a system. Eq. (4) is a mathematical way
of expressing this statement. This law is also a postulate, just
exactly as the first and second laws are.
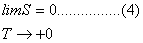
3.
An Unsuspected Visitor
Lets postulate the following ideal scenario for our analysis. There is an
extraterrestrial observer whose spacecraft is outside of our atmosphere and by
the way, he is never visible to us. However, in spite of the distance, he is
still able to distinguish the movement of individual human beings. Certainly,
it would not take too long for him, to realize that the movements of human
beings obey chaotic rules. This ideal scenario would not matter too much to
him, unless he ignores the second law of thermodynamics, but indeed he does
not ignore this law. Thus, such observer would conclude quickly that human
beings express many forms of unusual, seemingly irrational, behavior. For
example, he will be surprised looking at riots, political meetings, religious
behavior, wars, etc. As a result of these observations, he would ask himself,
what in hell motivates such uncommon behavior of the human beings?.
Suppose now that this alien visitor gets closer to the earth (remember, he is
invisible to human beings) and manages to learn the reason why the human
beings behave that way. Soon he would be able to understand that such
apparently unusual behavior is consistently motivated by a lack of some degree
of freedom; which may be summed up as a state of satisfaction or
dissatisfaction. Viewed in this way, our social system may be approached
through the second law of thermodynamics.
4.
Social Entropy as a
Pseudo State Function
Now, leaving the alien
visitor for a while. Our analysis induces us to think that Social
Entropy is essentially a function of social state, an expression
of the degree of satisfaction or dissatisfaction of human beings. This
state has to deal with the social, political, cultural and economic
situation . Thus, if we match appropriately the alien’s point of
view and our own experience toward the human social behavior, we find logical
to think on the application of the statistical form of the second law of
thermodynamics in order to calculate the social entropy .
5.
Formulating the Relationship to Calculate Social Entropy
We postulate the existence of
two types of contributions to the SE. First, what we name individual
contribution (DSb)
and second, the group contribution (DSg).
Consequently, we may write:
DSs=
DSb +
DSg
(5)
where SE=DSS
,
DSb may be
considered as a typical value, which characterizes base contribution. Strictly
speaking
DSb will
depend on such different contributions as the geographical location, racial
prejudices, religion, etc.
For practical purposes, being
DSb a relative
value, we may consider it as a constant for each particular human community at
a particular moment of history.
Now recalling Eq.(4)
DS’ = R ln
W
(6)
where
DS’ =
DSs-DSb;
N: total number of inhabitants in a chosen system (country), n: number of
people in a determined state (degree of dissatisfaction). Consequenrly, n=iN;
where i represent a fraction of N. Observe that
W is the characteristic
probability of the state of the system as we stated earlier, that is to say
the probability of the system (people of a country) to be in a particular mode
of agreement or dissagreement with the the current policital situation.
In order to simplify the application of (6) we use the Stirling formula and
find;
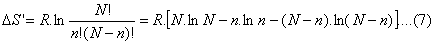
6.
A Case Study to Evaluate Social Entropy
In order to apply the
relationship given above, eq. (7), to the Peruvian case, we made use of public
information relative to the degree of satisfaction or dissatisfaction. This
information was relatively easy to be obtained through Internet by entering
web sites of specialized poll agencies. In fact, we found even more
interesting to show the increase of social entropy with increase of social
dissatisfaction in a rather broad range, instead of restricting
ourselves to a particular moment of history. Thus by straightforward
calculation using (7) we managed to produce a plot of social entropy vs.
degree of social dissatisfaction, see Fig.2.
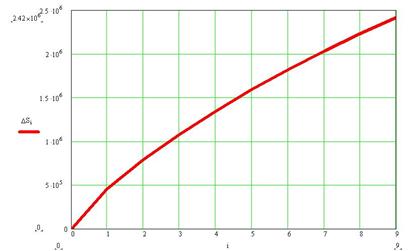
Degree of dissatisfaction
Fig 2. Social entropy increase
with social degree of dissatisfaction
For our calculation N was assumed to be 22 million and n ranged from 0
to 0.9.
7.
Discussion and Analysis
According to the Second Law of
Thermodynamics, the entropy of a naturally occurring system always increases.
If we use this statement to help to understand a human society, a question
arises immediately: Why is human society not chaotic on the whole?. The
answer appears to rely on society’s own ability to create organized systems
and sub systems by using intelligence. Let us take any well defined human
society for our analysis. A nation or any major political unit will do. We
know that there are rules that must be obeyed by all people in such a system
(at least in theory). These are the political laws that they obey. In
this way, political, economic, cultural and social rules must (or should) be
well defined and assembled in theory and practice in order to avoid / prevent
totally chaotic systems. To the extent that these laws are observed and
followed by the individuals within the system, the system will be orderly,
“regular” and avoid chaos. Those individuals who do NOT obey the laws
introduce disorder / chaos into the system. Thus the disorder is a precise
measure of expressed disagreement with and dissatisfaction with the rules /
laws of the society. All these variables may configure a social
response, that is to say, a degree of dissatisfaction or satisfaction with the
current system. As a matter of fact, if the social rules are arbitrarily
applied in favor of minorities, the social entropy will increase with time
more rapidly, compared to other social systems where justice favors no one and
applies to everyone, particularly to large majorities. Those who do not obey
are criminals, and must be dealt with as such. This forces conformity to the
laws, the rules of behavior, and applies a correction / motivation to prevent
chaos.
One of the key points for a
rapid increase of the social entropy is the degree of civil disobedience,
expressing information about internal dissatisfaction and encouraging chaos
and giving rise to the eventual “birth” of leaders in a particular scenario.
Consequently, we may see that social disorder comes from social
dissatisfaction, hence social entropy exists and may be calculated if we are
able to deduce mathematical relationships for it. Fortunately for us, we
did not have to dig too deep in order to find it.
Relative SE is possible to be
approached from a Boltzmann type relationship by using statistical data
concerning the degree of social dissatisfaction with the political system of a
country. The calculation shows a typical shape which becomes nearly asymptotic
on the large.
It is particularly interesting
to realize how dictatorial political regimes in the world collapse under the
same “mechanism”; that is to say a dictatorial collapsing patron. Where the
social entropy accumulates to a such extent that a small
perturbation conducts the system to a run away situation and the dictatorship
has to resign and scape.
Any political system that
permanently violates the Second Law of Thermodynamics, contributes itself to
increase its Social Entropy. In other words it forces itself to its end. We
may bring into account quite a lot of cases as examples. Thus, lets bring the
case of Sukarno´s regime in Indonesia, Marco´s regime in Philipines and
Fujimori´s regime in Perú.
Apparently, there are two ways
for a political system to force to an apparent social order, which is by being
honest and open, giving voluntary compliance with rules, or by making use of
the force, which is characteristic of dictatorial regimes; but the last one
works only for a very short period of time; because
DSb will start
increasing leading undoubtedly to the social dissatisfaction.
Human society has coined several
sayings which is a sophisticated way of stating the second law of
thermodynamics: remember for example: “There is no political malady
which will last 100 years, and there is nobody who will go along with it”(simply
because social entropy increases). Would you please remember Montesinos and
his “partner” as an pathetic example?. Or remember the disorder of Alan Garcia
before that?, just to rely on the Peruvian case.
8.
Concluding Remarks
SE exists and may be
approximated using a Boltzmann type equation.
SE apparently has two
components, one is the base contribution and the other is the group
contribution, both being important to be taken into account to fully
understand a particular moment of history and social behaviour.
SE may be estimated for any
social system because it measures the degree of social disagreement with the
current local administration. However, according to the uncertainty principle
and taking into account the “aliens point of view”, human beings are also
unpredictable; hence a degree of freedom should be added to the system in
study, just to increase the accuracy of the calculation. This approach has not
been performed here and will be dealt in future works.
The existence of SE implies that
the second law of thermodynamics may be applied to any society taking it
as a system ; although , we must be careful at getting reliable poll data in
rather long periods of time in order to be able to estimate an appropriate
answer. In this way, if we are able to show a scientific way of measuring the
social behaviour as the Social Entropy is in itself, we are eventually
producing a tool for the politicians no to treak people with such mistaking
information as stating that everything is all right.
9. References
1.
Thompson, Eduard. (1999). A Unified Introduction to Chemical
Engineering Thermodynamics. Stillwater Press, Orono, Maine, USA.
2.
Klotz, R. and Rosenberg, R. Chemical Thermodynamics, Basic Theory
and Methods (1994) , Fifth Edit. John Wiley and Sons Inc, USA.
3.
Palomino, Alfredo. Notas sobre Termodinámica Avanzada (2000),
UPG-UNSCH, Ayacucho, Perú.
4.
Krestóvnikov, A.N. and Vigdoróvich,V.N. Termodinámica Química
(1980) , Traducido del Ruso por Marco Navarrete; Edit. MIR, Moscú.
5.
Lawler,James. Notes on Advanced Topics in Thermodynamics(1989),
Unpublished book. Dallas, Texas, USA.
6. Kirillin, V.
, Sichev, V. and Sheindlin, A. (1976) Termodinámica Técnica, Traducido
del Ruso
por Antonio Molina, Edit. MIR, Moscú.
